Supplementary Analyses

Here, we report on our results on Preferred Relationship Options including Interest in Single Life; Interest in Sexual, Non-Romantic Relationships; Interest in Non-Monogamous Relationships; and Interest in Monogamous Relationships

Library

library(formr)
library(effects)

## Lade nötiges Paket: carData

## lattice theme set by effectsTheme()
## See ?effectsTheme for details.

library(effectsize)
library(lme4)

## Lade nötiges Paket: Matrix

library(sjstats)

## 
## Attache Paket: 'sjstats'

## Die folgenden Objekte sind maskiert von 'package:effectsize':
## 
##     cohens_f, cramers_v, phi

library(lmerTest)

## 
## Attache Paket: 'lmerTest'

## Das folgende Objekt ist maskiert 'package:lme4':
## 
##     lmer

## Das folgende Objekt ist maskiert 'package:stats':
## 
##     step

library(dplyr)

## 
## Attache Paket: 'dplyr'

## Die folgenden Objekte sind maskiert von 'package:formr':
## 
##     first, last

## Die folgenden Objekte sind maskiert von 'package:stats':
## 
##     filter, lag

## Die folgenden Objekte sind maskiert von 'package:base':
## 
##     intersect, setdiff, setequal, union

library(ggplot2)
library(RColorBrewer)
library(tidyverse)

## ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
## ✔ forcats   1.0.0     ✔ stringr   1.5.1
## ✔ lubridate 1.9.4     ✔ tibble    3.2.1
## ✔ purrr     1.0.2     ✔ tidyr     1.3.1
## ✔ readr     2.1.5

## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ tidyr::expand() masks Matrix::expand()
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::first()  masks formr::first()
## ✖ dplyr::lag()    masks stats::lag()
## ✖ dplyr::last()   masks formr::last()
## ✖ tidyr::pack()   masks Matrix::pack()
## ✖ tidyr::unpack() masks Matrix::unpack()
## ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

library(mgcv)         

## Lade nötiges Paket: nlme
## 
## Attache Paket: 'nlme'
## 
## Das folgende Objekt ist maskiert 'package:dplyr':
## 
##     collapse
## 
## Das folgende Objekt ist maskiert 'package:lme4':
## 
##     lmList
## 
## This is mgcv 1.9-1. For overview type 'help("mgcv-package")'.

library(stringr)     
library(sandwich)     
library(lmtest) 

## Lade nötiges Paket: zoo
## 
## Attache Paket: 'zoo'
## 
## Die folgenden Objekte sind maskiert von 'package:base':
## 
##     as.Date, as.Date.numeric

library(minqa)
library(tidyr)
library(ggpubr)
library(coefplot)
library(tibble)
library(purrr) # for running multiple regression
library(broom)

## 
## Attache Paket: 'broom'
## 
## Das folgende Objekt ist maskiert 'package:sjstats':
## 
##     bootstrap

library(mvmeta)

## This is mvmeta 1.0.3. For an overview type: help('mvmeta-package').

library(lm.beta)
library(countrycode)

apatheme = theme_bw() +
  theme(panel.grid.major = element_blank(),
        panel.grid.minor = element_blank(),
        panel.border = element_blank(),
        axis.line = element_line(),
        legend.title = element_blank(),
        plot.title = element_text(hjust = 0.5))

Main Analysis

Data

Load selected data based on 03_codebook

data_included_documented = read.csv(file = "data_included_documented.csv")[,-1]

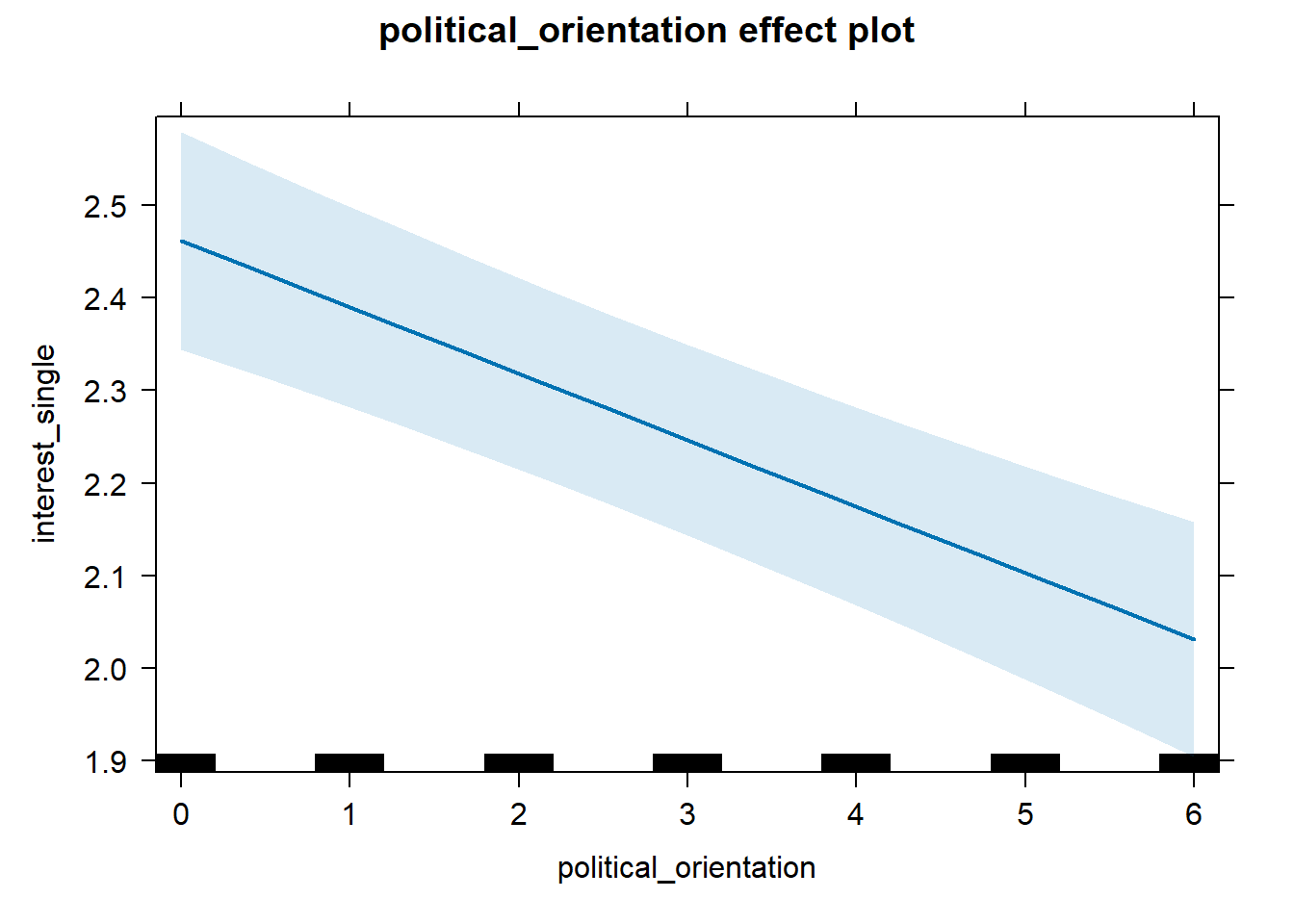
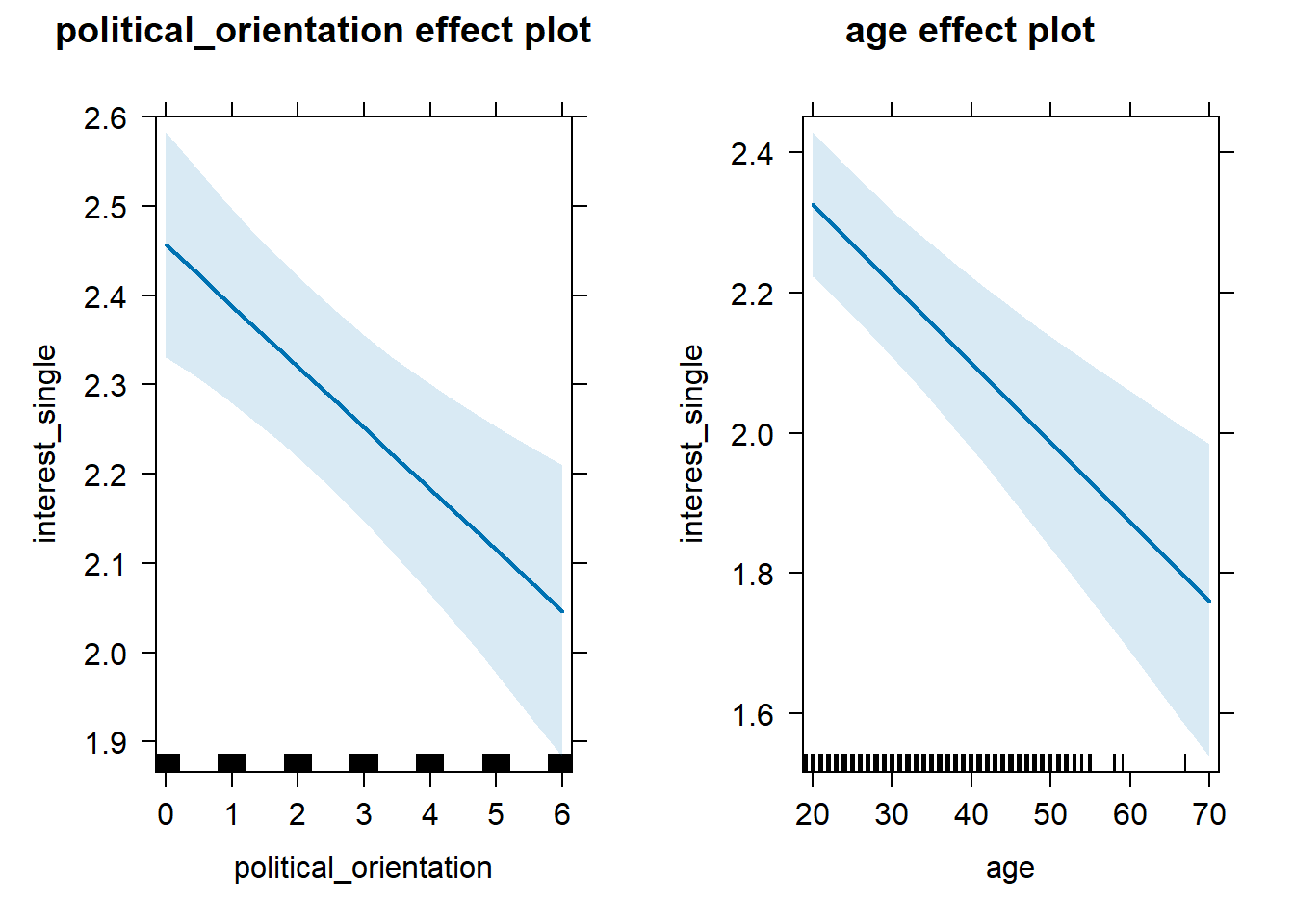
S1 Interest in Single Life

S1 There is a negative linear link between right-wing political orientation and women’s interest in being single.
Outcome: Ratings for interest in single life. Predictor: Political Orientation. Random intercept and random slope for country.

Models

model_interest_single <- lmer(interest_single ~ political_orientation + (1+political_orientation|country), data = data_included_documented, control =lmerControl(optimizer = "bobyqa"))

Summary

summary(model_interest_single)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: 
## interest_single ~ political_orientation + (1 + political_orientation |  
##     country)
##    Data: data_included_documented
## Control: lmerControl(optimizer = "bobyqa")
## 
## REML criterion at convergence: 51974.1
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -1.7078 -0.9823  0.0163  0.6611  2.7573 
## 
## Random effects:
##  Groups   Name                  Variance Std.Dev. Corr 
##  country  (Intercept)           0.116849 0.34183       
##           political_orientation 0.003378 0.05812  -0.16
##  Residual                       2.968827 1.72303       
## Number of obs: 13208, groups:  country, 144
## 
## Fixed effects:
##                       Estimate Std. Error       df t value Pr(>|t|)    
## (Intercept)            2.44485    0.06422 31.80915  38.068  < 2e-16 ***
## political_orientation -0.06556    0.01711 16.42094  -3.833  0.00141 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr)
## pltcl_rnttn -0.598

confint(model_interest_single, level = 0.997)

## Computing profile confidence intervals ...

##                           0.15 %      99.85 %
## .sig01                 0.1849826  0.579772477
## .sig02                -0.7990715  0.807232991
## .sig03                 0.0000000  0.140181840
## .sigma                 1.6919489  1.755120985
## (Intercept)            2.2391626  2.641095248
## political_orientation -0.1181832 -0.006601603

Standardized Coefficients

standardize_parameters(model_interest_single, method = "basic", ci = 0.997)

## # A tibble: 2 × 5
##   Parameter             Std_Coefficient    CI  CI_low CI_high
##   <chr>                           <dbl> <dbl>   <dbl>   <dbl>
## 1 (Intercept)                    0      0.997  0       0     
## 2 political_orientation         -0.0508 0.997 -0.0901 -0.0114

Plot

lmer(interest_single ~ political_orientation + (1 | country),
       data = data_included_documented) %>%
    allEffects() %>%
    plot()

S2 Interest in Sexual, Non-Romantic Relationships

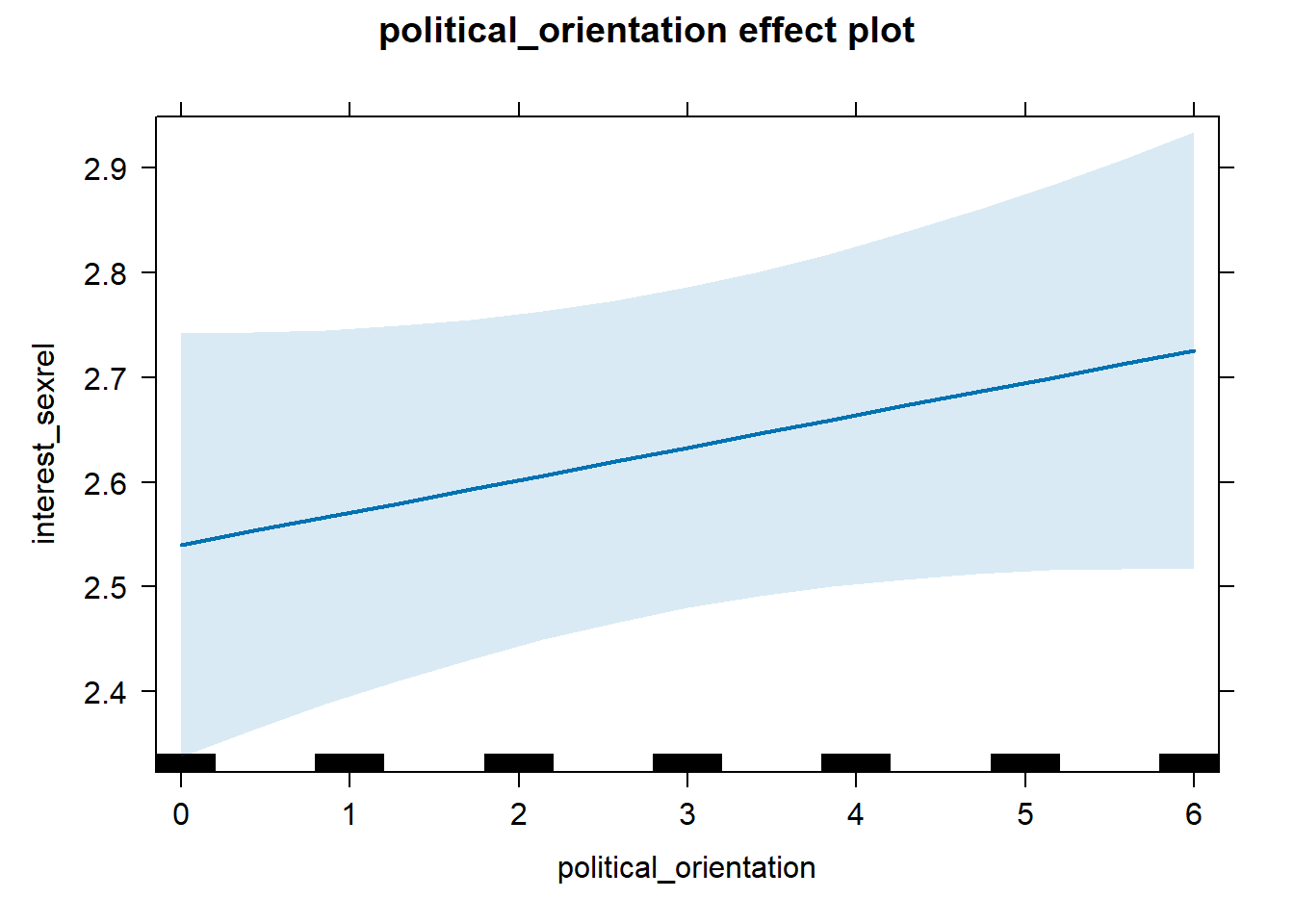
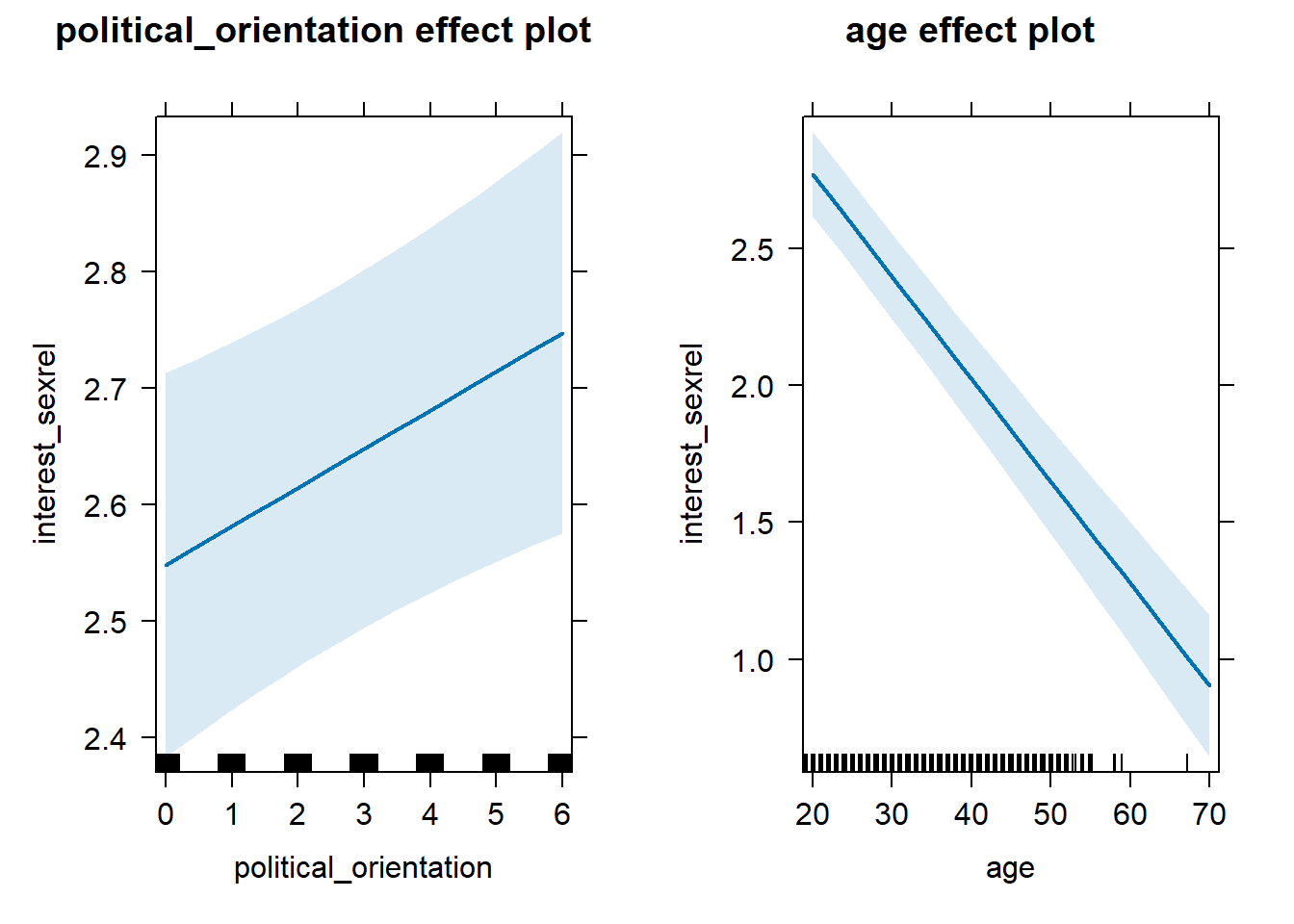
S2 There is a negative linear link between right-wing political orientation and women’s interest in having sexual, non-romantic relationships (e.g., hookups, one-night stands). Outcome: Ratings for interest in having sexual, non-romantic relationships. Predictor: Political Orientation. Random intercept and random slope for country.

Models

model_interest_sexrel <- lmer(interest_sexrel ~ political_orientation + (1+political_orientation|country), data = data_included_documented, control =lmerControl(optimizer = "bobyqa"))

Summary

summary(model_interest_sexrel)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: 
## interest_sexrel ~ political_orientation + (1 + political_orientation |  
##     country)
##    Data: data_included_documented
## Control: lmerControl(optimizer = "bobyqa")
## 
## REML criterion at convergence: 53552.6
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.76694 -0.83515 -0.02686  0.69705  2.48827 
## 
## Random effects:
##  Groups   Name                  Variance Std.Dev. Corr 
##  country  (Intercept)           0.54673  0.7394        
##           political_orientation 0.01011  0.1006   -0.52
##  Residual                       3.34229  1.8282        
## Number of obs: 13193, groups:  country, 144
## 
## Fixed effects:
##                       Estimate Std. Error       df t value Pr(>|t|)    
## (Intercept)            2.53992    0.10328 63.44029  24.592   <2e-16 ***
## political_orientation  0.03100    0.02327 25.94934   1.332    0.194    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr)
## pltcl_rnttn -0.654

confint(model_interest_sexrel, level = 0.997)

## Computing profile confidence intervals ...

##                            0.15 %   99.85 %
## .sig01                 0.51174594 1.0650785
## .sig02                -0.83709089 0.2309198
## .sig03                 0.03942878 0.2012493
## .sigma                 1.79514324 1.8622959
## (Intercept)            2.23004337 2.8581617
## political_orientation -0.04325027 0.1036027

Standardized Coefficients

standardize_parameters(model_interest_sexrel, method = "basic", ci = 0.997)

## # A tibble: 2 × 5
##   Parameter             Std_Coefficient    CI  CI_low CI_high
##   <chr>                           <dbl> <dbl>   <dbl>   <dbl>
## 1 (Intercept)                    0      0.997  0       0     
## 2 political_orientation          0.0213 0.997 -0.0262  0.0689

#ci(standardize_parameters(model_interest_sexrel, method = "basic"), ci = 0.997)

Plot

lmer(interest_sexrel ~ political_orientation + (1 + political_orientation| country),
       data = data_included_documented) %>%
    allEffects() %>%
    plot()

S3 Interest in Non-Monogamous Relationships

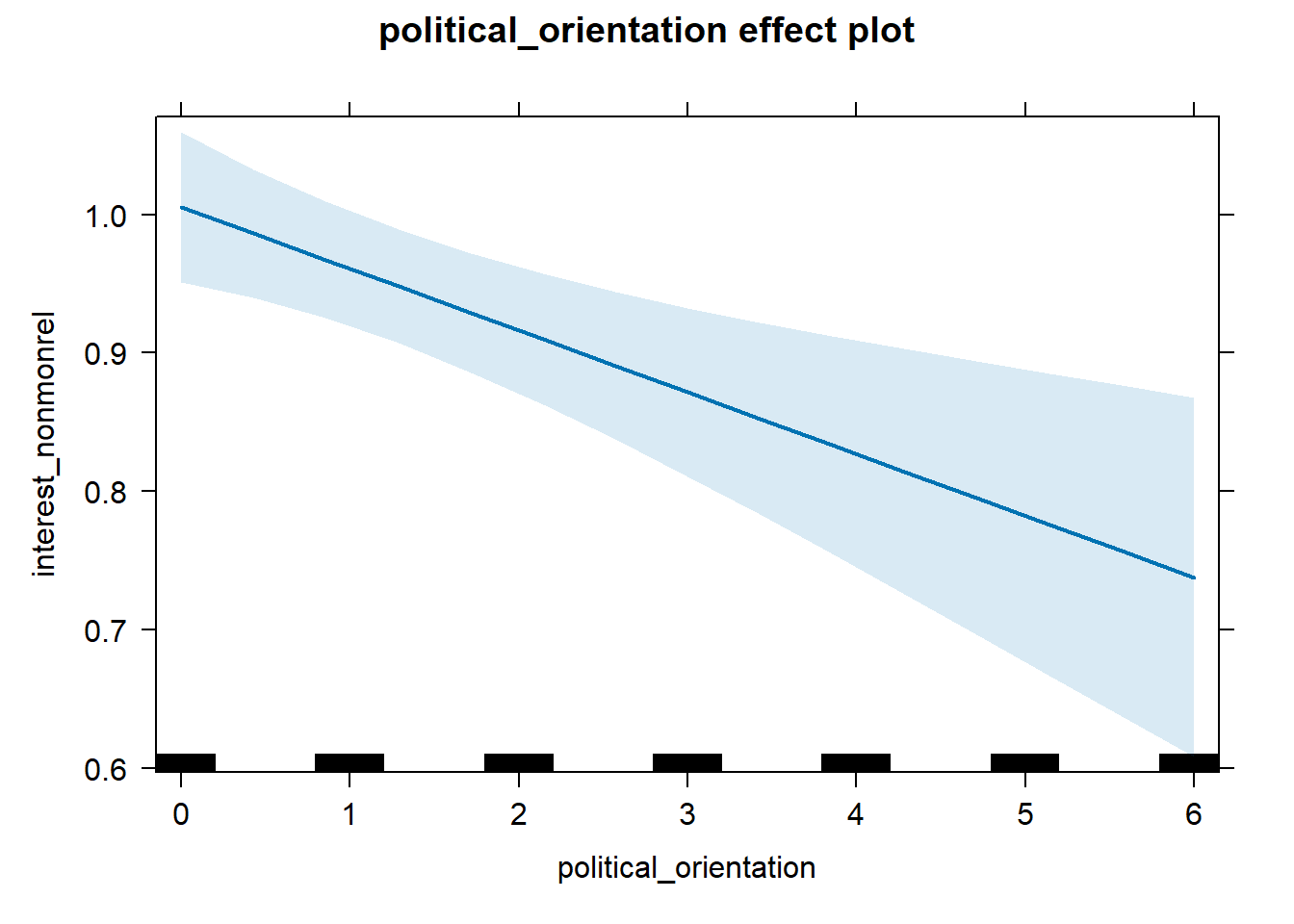
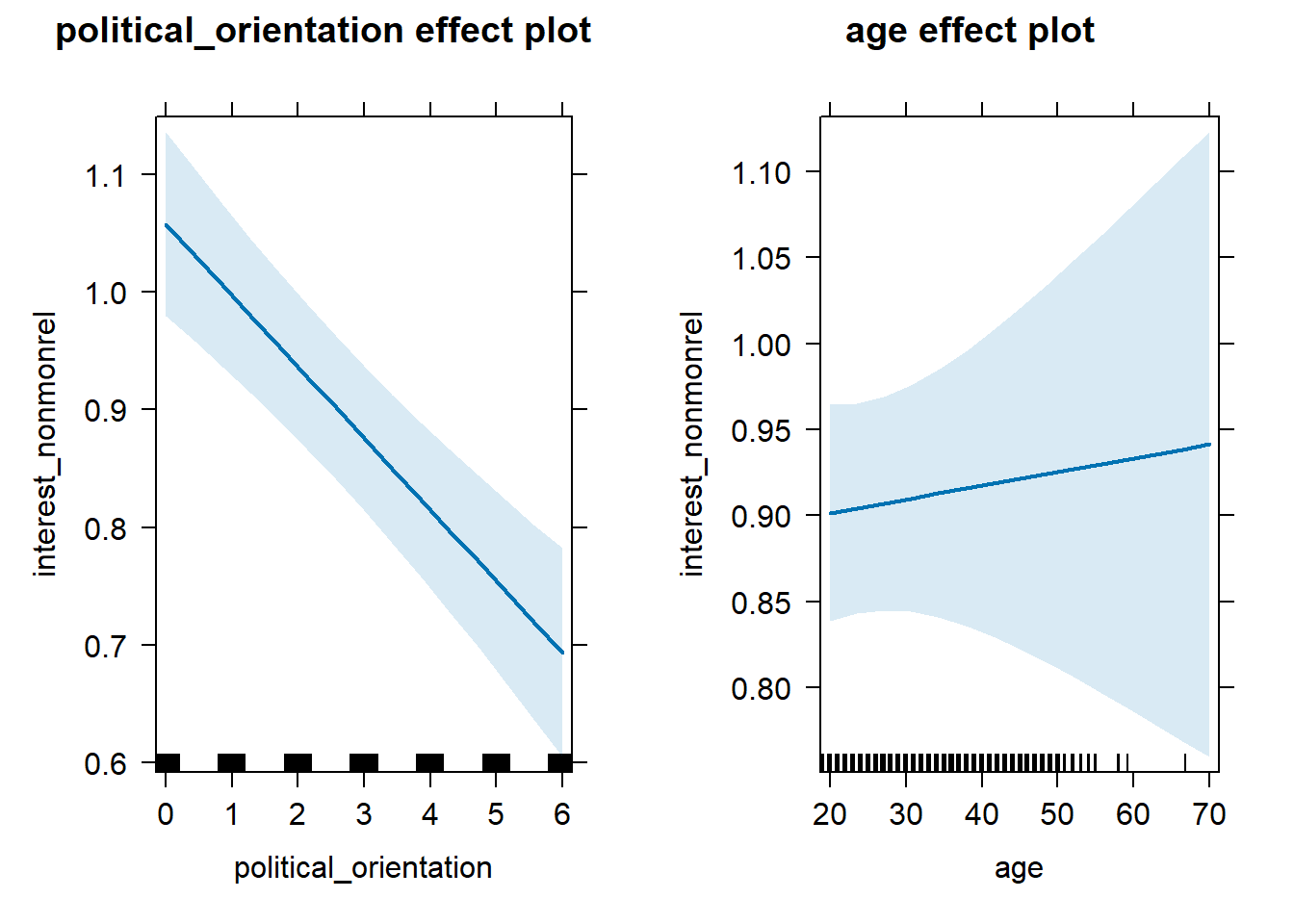
S3 There is a negative linear link between right-wing political orientation and women’s interest in having non-monogamous relationships. Outcome: Ratings for interest in having non-monogamous relationships. Predictor: Political Orientation. Random intercept and random slope for country.

Models

model_interest_nonmonrel <- lmer(interest_nonmonrel ~ political_orientation + (1+political_orientation|country), data = data_included_documented, control =lmerControl(optimizer = "bobyqa"))

Summary

summary(model_interest_nonmonrel)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: 
## interest_nonmonrel ~ political_orientation + (1 + political_orientation |  
##     country)
##    Data: data_included_documented
## Control: lmerControl(optimizer = "bobyqa")
## 
## REML criterion at convergence: 47749.3
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -0.9692 -0.5948 -0.4801  0.1749  3.8166 
## 
## Random effects:
##  Groups   Name                  Variance Std.Dev. Corr 
##  country  (Intercept)           0.036929 0.19217       
##           political_orientation 0.003119 0.05585  -0.57
##  Residual                       2.200558 1.48343       
## Number of obs: 13145, groups:  country, 144
## 
## Fixed effects:
##                       Estimate Std. Error       df t value Pr(>|t|)    
## (Intercept)            1.05078    0.04819 24.08063   21.81   <2e-16 ***
## political_orientation -0.05907    0.01550 21.31114   -3.81    0.001 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr)
## pltcl_rnttn -0.770

confint(model_interest_nonmonrel, level = 0.997)

## Computing profile confidence intervals ...

##                             0.15 %      99.85 %
## .sig01                 0.064398879  0.389501282
## .sig02                -0.923694403  0.985570830
## .sig03                 0.008087882  0.124709921
## .sigma                 1.456617726  1.511089379
## (Intercept)            0.893957781  1.200128299
## political_orientation -0.107312045 -0.008080654

Standardized Coefficients

standardize_parameters(model_interest_nonmonrel, method = "basic", ci = 0.997)

## # A tibble: 2 × 5
##   Parameter             Std_Coefficient    CI  CI_low CI_high
##   <chr>                           <dbl> <dbl>   <dbl>   <dbl>
## 1 (Intercept)                    0      0.997  0       0     
## 2 political_orientation         -0.0539 0.997 -0.0959 -0.0119

#ci(standardize_parameters(model_interest_nonmonrel, method = "basic"), ci = 0.997)

Plot

lmer(interest_nonmonrel ~ political_orientation + (1+political_orientation|country),
       data = data_included_documented) %>%
    allEffects() %>%
    plot()

## boundary (singular) fit: see help('isSingular')

S4 Interest in Monogamous Relationships

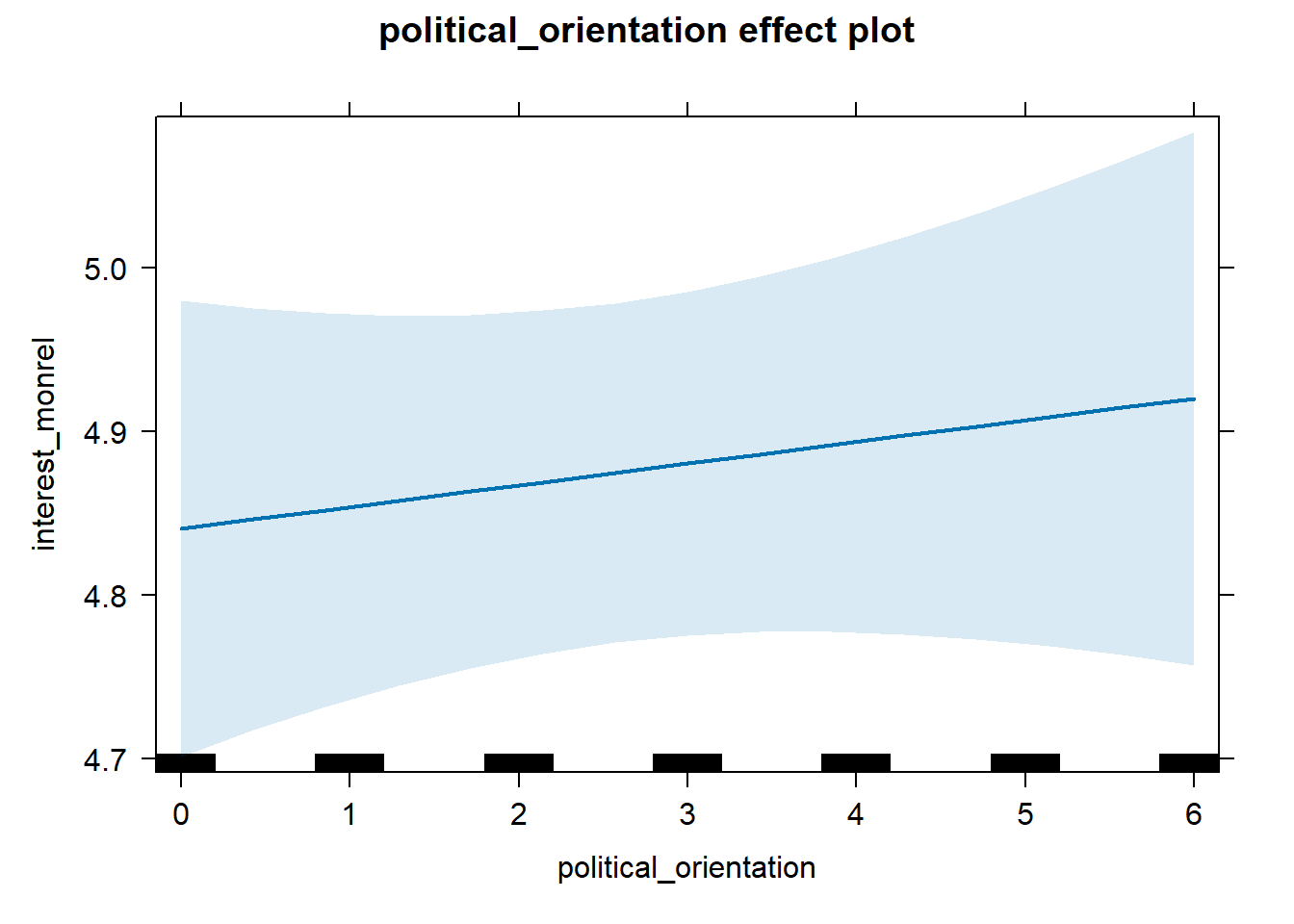
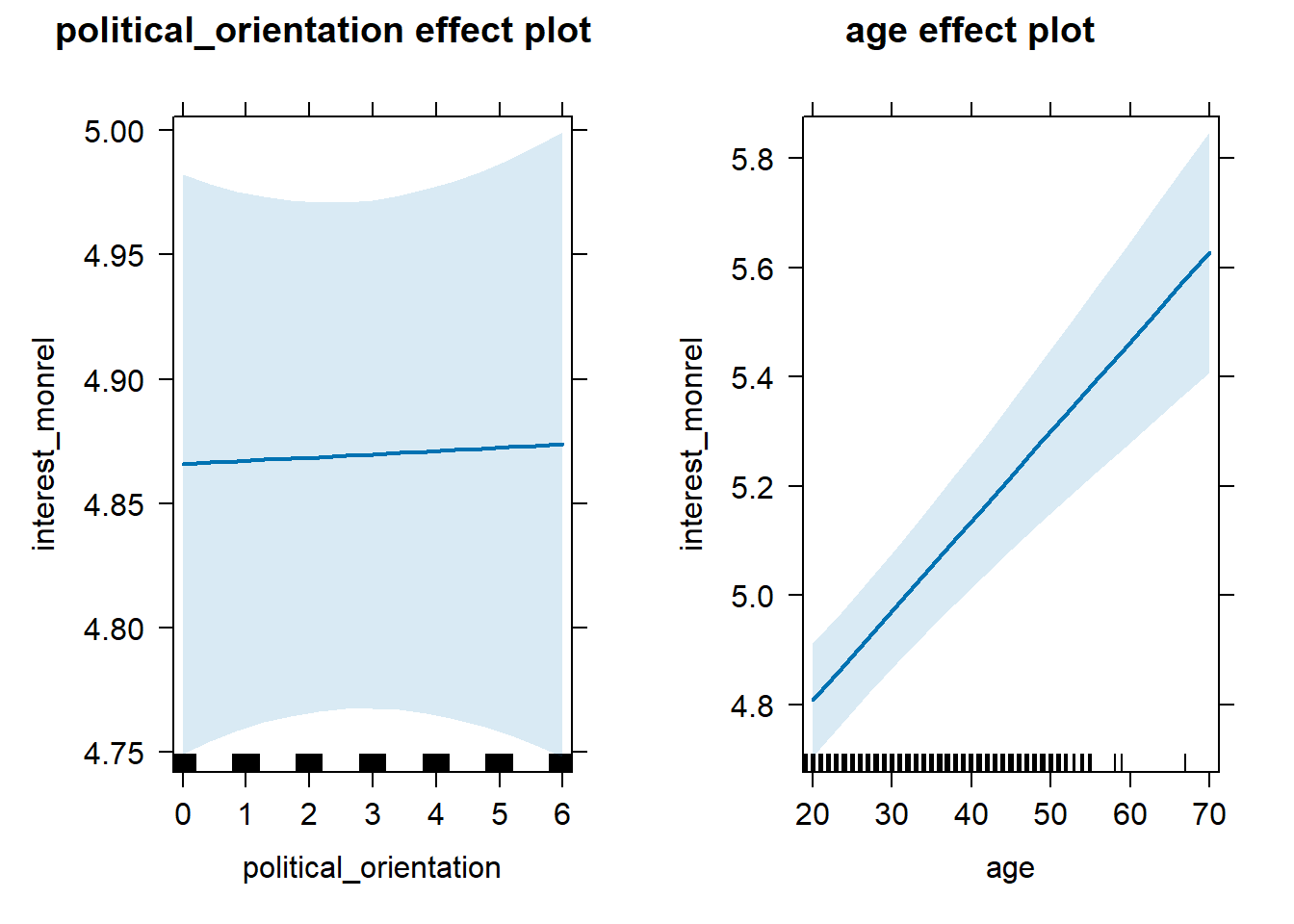
S4 There is no link between right-wing political orientation and women’s interest in having monogamous relationships. Outcome: Ratings for interest in having monogamous relationships. Predictor: Political Orientation. Random intercept and random slope for country.

Models

model_interest_monrel <- lmer(interest_monrel ~ political_orientation + (1+political_orientation|country), data = data_included_documented, control =lmerControl(optimizer = "bobyqa"))

Summary

summary(model_interest_monrel)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: 
## interest_monrel ~ political_orientation + (1 + political_orientation |  
##     country)
##    Data: data_included_documented
## Control: lmerControl(optimizer = "bobyqa")
## 
## REML criterion at convergence: 51454.1
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -3.1161 -0.3455  0.4959  0.6013  1.5791 
## 
## Random effects:
##  Groups   Name                  Variance Std.Dev. Corr 
##  country  (Intercept)           0.159956 0.39994       
##           political_orientation 0.004759 0.06899  -0.41
##  Residual                       2.888588 1.69958       
## Number of obs: 13165, groups:  country, 144
## 
## Fixed effects:
##                       Estimate Std. Error       df t value Pr(>|t|)    
## (Intercept)            4.84081    0.07114 27.75591  68.049   <2e-16 ***
## political_orientation  0.01324    0.01861 17.61097   0.711    0.486    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr)
## pltcl_rnttn -0.669

confint(model_interest_monrel, level = 0.997)

## Computing profile confidence intervals ...

##                            0.15 %    99.85 %
## .sig01                 0.22216840 0.69554009
## .sig02                -0.86699903 1.00000000
## .sig03                 0.01211041 0.15835921
## .sigma                 1.66887322 1.73134443
## (Intercept)            4.60723287 5.06149285
## political_orientation -0.04364710 0.08020918

Standardized Coefficients

standardize_parameters(model_interest_monrel, method = "basic", ci = 0.997)

## # A tibble: 2 × 5
##   Parameter             Std_Coefficient    CI  CI_low CI_high
##   <chr>                           <dbl> <dbl>   <dbl>   <dbl>
## 1 (Intercept)                    0      0.997  0       0     
## 2 political_orientation          0.0103 0.997 -0.0327  0.0534

#ci(standardize_parameters(model_interest_monrel, method = "basic"), ci = 0.997) #calculate by hand to get exact numbers

Plot

lmer(interest_monrel ~ political_orientation + (1+political_orientation|country),
       data = data_included_documented) %>%
    allEffects() %>%
    plot()

Robustness Analysis

Data

Load selected data based on 03_codebook

data_included_documented = read.csv(file = "data_included_documented.csv")[,-1]

S1 Interest in Single Life

S1 There is a negative linear link between right-wing political orientation and women’s interest in being single.
Outcome: Ratings for interest in single life. Predictors: Political Orientation & Age. Random intercept and random slope for country.

Models

model_interest_single_robustcheck <- lmer(interest_single ~ political_orientation + age + (1+political_orientation|country), data = data_included_documented, control =lmerControl(optimizer = "bobyqa"))

Summary

summary(model_interest_single_robustcheck)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: 
## interest_single ~ political_orientation + age + (1 + political_orientation |  
##     country)
##    Data: data_included_documented
## Control: lmerControl(optimizer = "bobyqa")
## 
## REML criterion at convergence: 51944.6
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -1.77221 -0.95685  0.02419  0.67012  2.76559 
## 
## Random effects:
##  Groups   Name                  Variance Std.Dev. Corr 
##  country  (Intercept)           0.117131 0.34224       
##           political_orientation 0.003592 0.05993  -0.16
##  Residual                       2.963381 1.72145       
## Number of obs: 13204, groups:  country, 144
## 
## Fixed effects:
##                         Estimate Std. Error         df t value Pr(>|t|)    
## (Intercept)            2.724e+00  8.445e-02  9.417e+01  32.261  < 2e-16 ***
## political_orientation -6.838e-02  1.733e-02  1.705e+01  -3.946  0.00104 ** 
## age                   -1.129e-02  2.204e-03  1.320e+04  -5.124 3.04e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) pltcl_
## pltcl_rnttn -0.478       
## age         -0.647  0.032

confint(model_interest_single_robustcheck, level = 0.997)

## Computing profile confidence intervals ...

## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): unexpected decrease in
## profile: using minstep

## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep
## Warning in nextpar(mat, cc, i, delta, lowcut, upcut): Last two rows have
## identical or NA .zeta values: using minstep

## Warning in FUN(X[[i]], ...): non-monotonic profile for .sig02

## Warning in confint.thpr(pp, level = level, zeta = zeta): bad spline fit for
## .sig02: falling back to linear interpolation

## Warning in regularize.values(x, y, ties, missing(ties), na.rm = na.rm):
## Reduktion auf einmalige 'x' Werte

##                            0.15 %      99.85 %
## .sig01                 0.18598545  0.579885456
## .sig02                -0.87343169  1.000000000
## .sig03                 0.00000000  0.141917484
## .sigma                 1.69032568  1.753447203
## (Intercept)            2.46746166  2.976973473
## political_orientation -0.12162835 -0.008907457
## age                   -0.01782619 -0.004743392

Standardized Coefficients

standardize_parameters(model_interest_single_robustcheck, method = "basic", ci = 0.997)

## # A tibble: 3 × 5
##   Parameter             Std_Coefficient    CI  CI_low CI_high
##   <chr>                           <dbl> <dbl>   <dbl>   <dbl>
## 1 (Intercept)                    0      0.997  0       0     
## 2 political_orientation         -0.0529 0.997 -0.0927 -0.0131
## 3 age                           -0.0441 0.997 -0.0697 -0.0186

#ci(standardize_parameters(model_interest_single_robustcheck, method = "basic"), ci = 0.997)

Plot

lmer(interest_single ~ political_orientation + age + (1+political_orientation|country),
       data = data_included_documented) %>%
    allEffects() %>%
    plot()

## Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
## Model failed to converge with max|grad| = 0.00264607 (tol = 0.002, component 1)

S2 Interest in Sexual, Non-Romantic Relationships

S2 There is a negative linear link between right-wing political orientation and women’s interest in having sexual, non-romantic relationships (e.g., hookups, one-night stands). Outcome: Ratings for interest in having sexual, non-romantic relationships. Predictors: Political Orientation & Age. Random intercept and random slope for country.

Models

model_interest_sexrel_robustcheck <- lmer(interest_sexrel ~ political_orientation + age + (1+political_orientation|country), data = data_included_documented, control =lmerControl(optimizer = "bobyqa"))

Summary

summary(model_interest_sexrel_robustcheck)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: 
## interest_sexrel ~ political_orientation + age + (1 + political_orientation |  
##     country)
##    Data: data_included_documented
## Control: lmerControl(optimizer = "bobyqa")
## 
## REML criterion at convergence: 53293.5
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.91783 -0.86031 -0.04707  0.71412  3.04454 
## 
## Random effects:
##  Groups   Name                  Variance Std.Dev. Corr 
##  country  (Intercept)           0.536147 0.73222       
##           political_orientation 0.009233 0.09609  -0.49
##  Residual                       3.278802 1.81075       
## Number of obs: 13189, groups:  country, 144
## 
## Fixed effects:
##                         Estimate Std. Error         df t value Pr(>|t|)    
## (Intercept)            3.465e+00  1.171e-01  1.142e+02  29.593   <2e-16 ***
## political_orientation  2.096e-02  2.265e-02  2.559e+01   0.925    0.364    
## age                   -3.715e-02  2.324e-03  1.316e+04 -15.987   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) pltcl_
## pltcl_rnttn -0.570       
## age         -0.494  0.028

confint(model_interest_sexrel_robustcheck, level = 0.997)

## Computing profile confidence intervals ...

##                            0.15 %     99.85 %
## .sig01                 0.51125710  1.04860121
## .sig02                -0.82654392  0.26568627
## .sig03                 0.03665801  0.19421010
## .sigma                 1.77793911  1.84445400
## (Intercept)            3.11630975  3.82004787
## political_orientation -0.05162425  0.09155244
## age                   -0.04405250 -0.03025721

Standardized Coefficients

standardize_parameters(model_interest_sexrel_robustcheck, method = "basic", ci = 0.997)

## # A tibble: 3 × 5
##   Parameter             Std_Coefficient    CI  CI_low CI_high
##   <chr>                           <dbl> <dbl>   <dbl>   <dbl>
## 1 (Intercept)                    0      0.997  0       0     
## 2 political_orientation          0.0144 0.997 -0.0319  0.0607
## 3 age                           -0.129  0.997 -0.153  -0.105

#ci(standardize_parameters(model_interest_sexrel_robustcheck, method = "basic"), ci = 0.997)
#calculate by hand to get exact numbers

Plot

lmer(interest_sexrel ~ political_orientation + age + (1|country),
       data = data_included_documented) %>%
    allEffects() %>%
    plot()

S3 Interest in Non-Monogamous Relationships

S3 There is a negative linear link between right-wing political orientation and women’s interest in having non-monogamous relationships. Outcome: Ratings for interest in having non-monogamous relationships. Predictors: Political Orientation & Age. Random intercept and random slope for country.

Models

model_interest_nonmonrel_robustcheck <- lmer(interest_nonmonrel ~ political_orientation + age + (1+political_orientation|country), data = data_included_documented, control =lmerControl(optimizer = "bobyqa"))

Summary

summary(model_interest_nonmonrel_robustcheck)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: 
## interest_nonmonrel ~ political_orientation + age + (1 + political_orientation |  
##     country)
##    Data: data_included_documented
## Control: lmerControl(optimizer = "bobyqa")
## 
## REML criterion at convergence: 47748.1
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -0.9724 -0.5972 -0.4791  0.1761  3.8178 
## 
## Random effects:
##  Groups   Name                  Variance Std.Dev. Corr 
##  country  (Intercept)           0.036904 0.19210       
##           political_orientation 0.003098 0.05566  -0.57
##  Residual                       2.201192 1.48364       
## Number of obs: 13141, groups:  country, 144
## 
## Fixed effects:
##                         Estimate Std. Error         df t value Pr(>|t|)    
## (Intercept)            1.033e+00  6.724e-02  8.872e+01  15.357  < 2e-16 ***
## political_orientation -5.884e-02  1.549e-02  2.136e+01  -3.798  0.00103 ** 
## age                    7.390e-04  1.899e-03  1.310e+04   0.389  0.69715    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) pltcl_
## pltcl_rnttn -0.573       
## age         -0.698  0.031

confint(model_interest_nonmonrel_robustcheck, level = 0.997)

## Computing profile confidence intervals ...

##                             0.15 %      99.85 %
## .sig01                 0.064113969  0.389476424
## .sig02                -0.923882439  0.759957786
## .sig03                 0.007668933  0.124407294
## .sigma                 1.456768369  1.511253817
## (Intercept)            0.827678660  1.233629191
## political_orientation -0.107023703 -0.007890225
## age                   -0.004899292  0.006375122

Standardized Coefficients

standardize_parameters(model_interest_nonmonrel_robustcheck, method = "basic", ci = 0.997)

## # A tibble: 3 × 5
##   Parameter             Std_Coefficient    CI  CI_low CI_high
##   <chr>                           <dbl> <dbl>   <dbl>   <dbl>
## 1 (Intercept)                   0       0.997  0       0     
## 2 political_orientation        -0.0537  0.997 -0.0956 -0.0117
## 3 age                           0.00340 0.997 -0.0226  0.0294

Plot

lmer(interest_nonmonrel ~ political_orientation + age + (1 | country),
       data = data_included_documented) %>%
    allEffects() %>%
    plot()

S4 Interest in Monogamous Relationships

S4 There is no link between right-wing political orientation and women’s interest in having monogamous relationships. Outcome: Ratings for interest in having monogamous relationships. Predictors: Political Orientation & Age. Random intercept and random slope for country.

Models

model_interest_monrel_robustcheck <- lmer(interest_monrel ~ political_orientation + age + (1+political_orientation|country), data = data_included_documented, control =lmerControl(optimizer = "bobyqa"))

Summary

summary(model_interest_monrel_robustcheck)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: 
## interest_monrel ~ political_orientation + age + (1 + political_orientation |  
##     country)
##    Data: data_included_documented
## Control: lmerControl(optimizer = "bobyqa")
## 
## REML criterion at convergence: 51395.4
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -3.3078 -0.3357  0.4511  0.6122  1.6180 
## 
## Random effects:
##  Groups   Name                  Variance Std.Dev. Corr 
##  country  (Intercept)           0.149360 0.38647       
##           political_orientation 0.004552 0.06747  -0.37
##  Residual                       2.877455 1.69631       
## Number of obs: 13161, groups:  country, 144
## 
## Fixed effects:
##                        Estimate Std. Error        df t value Pr(>|t|)    
## (Intercept)           4.435e+00  8.808e-02 6.914e+01  50.349  < 2e-16 ***
## political_orientation 1.756e-02  1.838e-02 1.723e+01   0.955    0.353    
## age                   1.636e-02  2.174e-03 1.315e+04   7.526 5.58e-14 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) pltcl_
## pltcl_rnttn -0.540       
## age         -0.612  0.031

confint(model_interest_monrel_robustcheck, level = 0.997)

## Computing profile confidence intervals ...

##                            0.15 %    99.85 %
## .sig01                 0.21515994 0.67856164
## .sig02                -0.85879483 0.89318148
## .sig03                 0.01048347 0.15671408
## .sigma                 1.66558877 1.72794152
## (Intercept)            4.16017509 4.70168722
## political_orientation -0.03844329 0.08417633
## age                    0.00991095 0.02281649

Standardized Coefficients

standardize_parameters(model_interest_monrel_robustcheck, method = "basic", ci = 0.997)

## # A tibble: 3 × 5
##   Parameter             Std_Coefficient    CI  CI_low CI_high
##   <chr>                           <dbl> <dbl>   <dbl>   <dbl>
## 1 (Intercept)                    0      0.997  0       0     
## 2 political_orientation          0.0137 0.997 -0.0289  0.0562
## 3 age                            0.0644 0.997  0.0390  0.0899

Plot

lmer(interest_monrel ~ political_orientation + age + (1| country),
       data = data_included_documented) %>%
    allEffects() %>%
    plot()

Exploratory Analysis for Countries

Data

Load selected data based on 03_codebook

data_included_documented = read.csv(file = "data_included_documented.csv")[,-1]

Inclusion of Data

countries = as.data.frame(table(data_included_documented$country)) %>%
  arrange(-Freq)

countries

## # A tibble: 144 × 2
##    Var1                      Freq
##    <fct>                    <int>
##  1 France                    2013
##  2 Germany                   1846
##  3 United States of America  1254
##  4 Mexico                    1157
##  5 Italy                      968
##  6 Brazil                     806
##  7 Spain                      562
##  8 United Kingdom             499
##  9 Denmark                    395
## 10 Colombia                   387
## # ℹ 134 more rows

We will include all countries with more than 500 participants. This allows us to show effect sizes for a diverse range of countries. Diversity of countries is indicated by:

• location: European (France, Germany, Italy, Spain); North American (United States of America); South American (Mexico, Brazil)
• language: French (France); German (Germany); English (United States of America); Spanish (Mexico, Spain); Italian (Italy); Portuguese (Brazil)
• culture: Western (France, Germany, Italy, Spain, United States of America); Non-Western (Mexico, Brazil)

Sample sizes of other countries are too small (n < 500) to reach any conclusions.

seven_countries = countries %>% filter(Freq > 500)
data_included_documented_rescon = data_included_documented %>%
  filter(country %in% seven_countries$Var1)

countries_rescon =
  data_included_documented_rescon %>%
  select(country) %>%
  table() %>%
  as.data.frame() %>%
  arrange(-Freq)


countries_rescon

## # A tibble: 7 × 2
##   country                   Freq
##   <fct>                    <int>
## 1 France                    2013
## 2 Germany                   1846
## 3 United States of America  1254
## 4 Mexico                    1157
## 5 Italy                      968
## 6 Brazil                     806
## 7 Spain                      562

Models

S1 Interest in Single Life

data_included_documented_rescon_wide = data_included_documented_rescon %>%
  pivot_wider(names_from = country, values_from = political_orientation) %>%
  select(interest_single, France, Germany, `United States of America`, Mexico,
         Italy, Brazil, Spain)

models_interest_single = data_included_documented_rescon_wide %>%
  select(-interest_single) %>%
  map(~lm(data_included_documented_rescon_wide$interest_single ~ .x,
      data = data_included_documented_rescon_wide)) %>%
  map(lm.beta)

models_interest_single_coef = models_interest_single %>%
  map(coef) %>%
  as.data.frame() %>%
  rownames_to_column(var = "rowname") %>%
  filter(rowname != "(Intercept)") %>%
  pivot_longer(cols = -rowname) %>%
  select(-rowname) %>%
  rename(mean = value)

models_interest_single_se = models_interest_single %>%
  map(tidy) %>%
  tibble(models_pref_politicalsim_lin_se = ., Names = names(.)) %>%
  hoist(models_pref_politicalsim_lin_se, coefficients = "std.error") %>%
  select(-models_pref_politicalsim_lin_se) %>%
  unnest_wider(., coefficients, names_sep = "_") %>%
  select(coefficients_2, Names) %>%
  rename("name" = "Names",
         "se" = "coefficients_2") %>%
  mutate(name = ifelse(name == "United States of America",
                       "United.States.of.America", name))



models_interest_single_analyses = left_join(models_interest_single_coef,
                                            models_interest_single_se,
                                            by = "name") %>%
  mutate(outcome = "S1 Interest in Single Life")

countries_rescon =
  data_included_documented_rescon %>%
  filter(!is.na(interest_single)) %>%
  select(country) %>%
  table() %>%
  as.data.frame() %>%
  arrange(-Freq)

models_interest_single_analyses$n = countries_rescon$Freq
sum(models_interest_single_analyses$n)

## [1] 8577

model = mvmeta(mean ~ 1, data = models_interest_single_analyses, S = se^2,
               method = "fixed")
summary(model)

## Call:  mvmeta(formula = mean ~ 1, S = se^2, data = models_interest_single_analyses, 
##     method = "fixed")
## 
## Univariate fixed-effects meta-analysis
## Dimension: 1
## 
## Fixed-effects coefficients
##              Estimate  Std. Error        z  Pr(>|z|)  95%ci.lb  95%ci.ub     
## (Intercept)   -0.0614      0.0136  -4.5225    0.0000   -0.0881   -0.0348  ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 
## 
## Univariate Cochran Q-test for heterogeneity:
## Q = 8.4415 (df = 6), p-value = 0.2075
## I-square statistic = 28.9%
## 
## 7 studies, 7 observations, 1 fixed and 0 random-effects parameters
##   logLik       AIC       BIC  
##  12.4542  -22.9084  -22.9624

S2 Interest in Sexual, Non-Romantic Relationships

data_included_documented_rescon_wide = data_included_documented_rescon %>%
  pivot_wider(names_from = country, values_from = political_orientation) %>%
  select(interest_sexrel, France, Germany, `United States of America`, Mexico,
         Italy, Brazil, Spain)

models_interest_sexrel = data_included_documented_rescon_wide %>%
  select(-interest_sexrel) %>%
  map(~lm(data_included_documented_rescon_wide$interest_sexrel ~ .x,
      data = data_included_documented_rescon_wide)) %>%
  map(lm.beta)

models_interest_sexrel_coef = models_interest_sexrel %>%
  map(coef) %>%
  as.data.frame() %>%
  rownames_to_column(var = "rowname") %>%
  filter(rowname != "(Intercept)") %>%
  pivot_longer(cols = -rowname) %>%
  select(-rowname) %>%
  rename(mean = value)

models_interest_sexrel_se = models_interest_sexrel %>%
  map(tidy) %>%
  tibble(models_pref_politicalsim_lin_se = ., Names = names(.)) %>%
  hoist(models_pref_politicalsim_lin_se, coefficients = "std.error") %>%
  select(-models_pref_politicalsim_lin_se) %>%
  unnest_wider(., coefficients, names_sep = "_") %>%
  select(coefficients_2, Names) %>%
  rename("name" = "Names",
         "se" = "coefficients_2") %>%
  mutate(name = ifelse(name == "United States of America",
                       "United.States.of.America", name))



models_interest_sexrel_analyses = left_join(models_interest_sexrel_coef,
                                            models_interest_sexrel_se,
                                            by = "name") %>%
  mutate(outcome = "S2 Interest in Sexual, Non-Romantic Relationships")

countries_rescon =
  data_included_documented_rescon %>%
  filter(!is.na(interest_sexrel)) %>%
  select(country) %>%
  table() %>%
  as.data.frame() %>%
  arrange(-Freq)

models_interest_sexrel_analyses$n = countries_rescon$Freq
sum(models_interest_sexrel_analyses$n)

## [1] 8567

model = mvmeta(mean ~ 1, data = models_interest_sexrel_analyses, S = se^2,
               method = "fixed")
summary(model)

## Call:  mvmeta(formula = mean ~ 1, S = se^2, data = models_interest_sexrel_analyses, 
##     method = "fixed")
## 
## Univariate fixed-effects meta-analysis
## Dimension: 1
## 
## Fixed-effects coefficients
##              Estimate  Std. Error       z  Pr(>|z|)  95%ci.lb  95%ci.ub   
## (Intercept)    0.0356      0.0145  2.4579    0.0140    0.0072    0.0640  *
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 
## 
## Univariate Cochran Q-test for heterogeneity:
## Q = 23.8985 (df = 6), p-value = 0.0005
## I-square statistic = 74.9%
## 
## 7 studies, 7 observations, 1 fixed and 0 random-effects parameters
##  logLik      AIC      BIC  
##  4.2988  -6.5976  -6.6516

S3 Interest in Non-Monogamous Relationships

data_included_documented_rescon_wide = data_included_documented_rescon %>%
  pivot_wider(names_from = country, values_from = political_orientation) %>%
  select(interest_nonmonrel, France, Germany, `United States of America`, Mexico,
         Italy, Brazil, Spain)

models_interest_nonmonrel = data_included_documented_rescon_wide %>%
  select(-interest_nonmonrel) %>%
  map(~lm(data_included_documented_rescon_wide$interest_nonmonrel ~ .x,
      data = data_included_documented_rescon_wide)) %>%
  map(lm.beta)

models_interest_nonmonrel_coef = models_interest_nonmonrel %>%
  map(coef) %>%
  as.data.frame() %>%
  rownames_to_column(var = "rowname") %>%
  filter(rowname != "(Intercept)") %>%
  pivot_longer(cols = -rowname) %>%
  select(-rowname) %>%
  rename(mean = value)

models_interest_nonmonrel_se = models_interest_nonmonrel %>%
  map(tidy) %>%
  tibble(models_pref_politicalsim_lin_se = ., Names = names(.)) %>%
  hoist(models_pref_politicalsim_lin_se, coefficients = "std.error") %>%
  select(-models_pref_politicalsim_lin_se) %>%
  unnest_wider(., coefficients, names_sep = "_") %>%
  select(coefficients_2, Names) %>%
  rename("name" = "Names",
         "se" = "coefficients_2") %>%
  mutate(name = ifelse(name == "United States of America",
                       "United.States.of.America", name))



models_interest_nonmonrel_analyses = left_join(models_interest_nonmonrel_coef,
                                            models_interest_nonmonrel_se,
                                            by = "name") %>%
  mutate(outcome = "S3 Interest in Non-Monogamous Relationships")

countries_rescon =
  data_included_documented_rescon %>%
  filter(!is.na(interest_nonmonrel)) %>%
  select(country) %>%
  table() %>%
  as.data.frame() %>%
  arrange(-Freq)

models_interest_nonmonrel_analyses$n = countries_rescon$Freq
sum(models_interest_nonmonrel_analyses$n)

## [1] 8537

model = mvmeta(mean ~ 1, data = models_interest_nonmonrel_analyses, S = se^2,
               method = "fixed")
summary(model)

## Call:  mvmeta(formula = mean ~ 1, S = se^2, data = models_interest_nonmonrel_analyses, 
##     method = "fixed")
## 
## Univariate fixed-effects meta-analysis
## Dimension: 1
## 
## Fixed-effects coefficients
##              Estimate  Std. Error        z  Pr(>|z|)  95%ci.lb  95%ci.ub     
## (Intercept)   -0.0675      0.0112  -6.0030    0.0000   -0.0896   -0.0455  ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 
## 
## Univariate Cochran Q-test for heterogeneity:
## Q = 18.3263 (df = 6), p-value = 0.0055
## I-square statistic = 67.3%
## 
## 7 studies, 7 observations, 1 fixed and 0 random-effects parameters
##   logLik       AIC       BIC  
##   8.6479  -15.2957  -15.3498

S4 Interest in Monogamous Relationships

data_included_documented_rescon_wide = data_included_documented_rescon %>%
  pivot_wider(names_from = country, values_from = political_orientation) %>%
  select(interest_monrel, France, Germany, `United States of America`, Mexico,
         Italy, Brazil, Spain)

models_interest_monrel = data_included_documented_rescon_wide %>%
  select(-interest_monrel) %>%
  map(~lm(data_included_documented_rescon_wide$interest_monrel ~ .x,
      data = data_included_documented_rescon_wide)) %>%
  map(lm.beta)

models_interest_monrel_coef = models_interest_monrel %>%
  map(coef) %>%
  as.data.frame() %>%
  rownames_to_column(var = "rowname") %>%
  filter(rowname != "(Intercept)") %>%
  pivot_longer(cols = -rowname) %>%
  select(-rowname) %>%
  rename(mean = value)

models_interest_monrel_se = models_interest_monrel %>%
 map(tidy) %>%
  tibble(models_pref_politicalsim_lin_se = ., Names = names(.)) %>%
  hoist(models_pref_politicalsim_lin_se, coefficients = "std.error") %>%
  select(-models_pref_politicalsim_lin_se) %>%
  unnest_wider(., coefficients, names_sep = "_") %>%
  select(coefficients_2, Names) %>%
  rename("name" = "Names",
         "se" = "coefficients_2") %>%
  mutate(name = ifelse(name == "United States of America",
                       "United.States.of.America", name))



models_interest_monrel_analyses = left_join(models_interest_monrel_coef,
                                            models_interest_monrel_se,
                                            by = "name") %>%
  mutate(outcome = "S4 Interest in Monogamous Relationships")

countries_rescon =
  data_included_documented_rescon %>%
  filter(!is.na(interest_monrel)) %>%
  select(country) %>%
  table() %>%
  as.data.frame() %>%
  arrange(-Freq)

models_interest_monrel_analyses$n = countries_rescon$Freq
sum(models_interest_monrel_analyses$n)

## [1] 8548

model = mvmeta(mean ~ 1, data = models_interest_monrel_analyses, S = se^2,
               method = "fixed")
summary(model)

## Call:  mvmeta(formula = mean ~ 1, S = se^2, data = models_interest_monrel_analyses, 
##     method = "fixed")
## 
## Univariate fixed-effects meta-analysis
## Dimension: 1
## 
## Fixed-effects coefficients
##              Estimate  Std. Error        z  Pr(>|z|)  95%ci.lb  95%ci.ub   
## (Intercept)   -0.0048      0.0133  -0.3588    0.7197   -0.0307    0.0212   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 
## 
## Univariate Cochran Q-test for heterogeneity:
## Q = 9.1679 (df = 6), p-value = 0.1644
## I-square statistic = 34.6%
## 
## 7 studies, 7 observations, 1 fixed and 0 random-effects parameters
##   logLik       AIC       BIC  
##  12.0307  -22.0613  -22.1154

Exploratory Analysis for Regions

Data

Load selected data based on 03_codebook

data_included_documented = read.csv(file = "data_included_documented.csv")[,-1]

Inclusion of Data

data_included_documented <- data_included_documented %>%
  mutate(region1 = countrycode(country,
                                 origin = "country.name",
                                 destination = "region"),
         region1 = ifelse(country == "Micronesia",
                            "East Asia and Pacific",
                            region1),
         region2 = countrycode(country,
                                 origin = "country.name",
                                 destination = "continent"),
         region2 = ifelse(country == "Micronesia",
                            "Oceania",
                            region2))

## Warning: There were 2 warnings in `mutate()`.
## The first warning was:
## ℹ In argument: `region1 = countrycode(country, origin = "country.name",
##   destination = "region")`.
## Caused by warning:
## ! Some values were not matched unambiguously: Micronesia
## ℹ Run `dplyr::last_dplyr_warnings()` to see the 1 remaining warning.

table(data_included_documented$region1)

## 
##        East Asia & Pacific      East Asia and Pacific 
##                        674                          1 
##      Europe & Central Asia  Latin America & Caribbean 
##                       7441                       3325 
## Middle East & North Africa              North America 
##                         90                       1592 
##                 South Asia         Sub-Saharan Africa 
##                         59                         75

table(data_included_documented$region2)

## 
##   Africa Americas     Asia   Europe  Oceania 
##      108     4917      645     7417      170

data_included_documented = data_included_documented %>%
  mutate(region_final = ifelse(region2 == "Africa", "Africa",
                                  ifelse(region2 == "Asia", "Asia",
                                         ifelse(region2 == "Europe", "Europe",
                           ifelse(region2 == "Oceania", "Oceania",
                                  ifelse(region1 == "Latin America & Caribbean",
                                         "Latin and South America",
                                         ifelse(region1 == "North America",
                                                "North America", NA)))))))

data_included_documented <- data_included_documented %>%
  mutate(region_final = ifelse(country %in% c("Afghanistan", "Bahrain", "Iran",
                                                 "Iraq", "Israel", "Jordan", 
                                                 "Kazakhstan", "Kuwait", "Kyrgyzstan",
                                                 "Lebanon", "Pakistan", 
                                                 "Palestinian Territories", "Qatar",
                                                 "Saudi Arabia", "Syria", 
                                                 "Turkey", "Turkmenistan",
                                                 "United Arab Emirates", "Indonesia"),
                                  "Middle East and Central Asia", region_final),
         region_final = ifelse(country %in% c("Armenia", "Burma",
                                                 "China",
                                                 "East Timor (see Timor-Leste)", 
                                                 "Georgia", "Hong Kong", "India",
                                                 "Japan", "Malaysia", "Maldives",
                                                 "Nepal", "Philippines", "Singapore",
                                                 "South Korea", "Sri Lanka", 
                                                 "Taiwan", "Thailand", "Vietnam"), 
                                  "South and East Asia", region_final))

x <- data_included_documented %>% 
  select(country, region_final) %>%
  group_by(country, region_final) %>%
  summarize(n = n()) %>%
  arrange(region_final, country)

## `summarise()` has grouped output by 'country'. You can override using the
## `.groups` argument.

write.csv2(x, file = "country_regions.csv")

regions <- x %>%
  group_by(region_final) %>%
  summarize(countries = n(),
            participants = sum(n))

regions

## # A tibble: 7 × 3
##   region_final                 countries participants
##   <chr>                            <int>        <int>
## 1 Africa                              26          108
## 2 Europe                              41         7417
## 3 Latin and South America             33         3325
## 4 Middle East and Central Asia        19          103
## 5 North America                        2         1592
## 6 Oceania                              5          170
## 7 South and East Asia                 18          542

We will include all regions with more than 500 participants. This allows us to show effect sizes for a diverse range of regions.

These regions include the following countries (n)

Europe included 41 countries: France (n = 2,013); Germany (n = 1,846); Italy (n = 968); Spain (n = 562); United Kingdom (n = 499); Denmark (n = 395); Switzerland (n = 280); Austria (n = 197); Russia (n = 155); Belgium (n = 102); Ireland (n = 59); Portugal (n = 51); Netherlands (n = 44); Finland (n = 31); Sweden (n = 27); Romania (n = 24); Ukraine (n = 21); Belarus (n = 13); Luxembourg (n = 13); Estonia (n = 12); Norway (n = 12); Czechia (n = 11); Bulgaria (n = 9); Hungary (n = 9); Latvia (n = 8); Poland (n = 7); Andorra (n = 6); Bosnia and Herzegovina (n = 6); Croatia (n = 6); Iceland (n = 5); Serbia (n = 5); Greece (n = 4); Lithuania (n = 3); Slovakia (n = 3); Slovenia (n = 3); Albania (n = 2); Malta (n = 2); Liechtenstein (n = 1); Macedonia (n = 1); Monaco (n = 1); and Montenegro (n = 1).

Latin and South America included 33 countries: Mexico (n = 1157); Brazil (n = 806); Colombia (n = 387); Argentina (n = 217); Chile (n = 154); Peru (n = 119); Ecuador (n = 102); Venezuela (n = 67); Guatemala (n = 61); Costa Rica (n = 47); Dominican Republic (n = 41); El Salvador (n = 26); Uruguay (n = 24); Bolivia (n = 23); Honduras (n = 18); Nicaragua (n = 15); Panama (n = 15); Paraguay (n = 11); Trinidad and Tobago (n = 8); Jamaica (n = 6); Haiti (n = 4); Guyana (n = 3); Antigua and Barbuda (n = 2); Dominica (n = 2); Saint Lucia (n = 2); Aruba (n = 1); Bahamas (n = 1); Barbados (n = 1); Belize (n = 1); Cuba (n = 1); Grenada (n = 1); Saint Vincent and the Grenadines (n = 1); and Sint Maarten (n = 1).

North America included 2 countries: United States of America (n = 1254) and Canada (n = 338).

South and East Asia included 18 countries: Japan (n = 290); China (n = 90); India (n = 45); Philippines (n = 36); Singapore (n = 26); Malaysia (n = 17); Hong Kong (n = 8); Taiwan (n = 7); South Korea (n = 5); Thailand (n = 4); Georgia (n = 3); Sri Lanka (n = 3); Armenia (n = 2); Vietnam (n = 2); Burma (n = 1); East Timor (n = 1); Maldives (n = 1); and Nepal (n = 1).

Oceania included 5 countries: Australia (n = 133); New Zealand (n = 34); Fiji (n = 1); Marshall Islands (n = 1); and Micronesia (n = 1).

Africa included 26 countries: South Africa (n = 29); Morocco (n = 16); Algeria (n = 7); Tunisia (n = 7); Kenya (n = 6); Nigeria (n = 6); Senegal (n = 5); Namibia (n = 4); Cameroon (n = 3); Egypt (n = 3); Ghana (n = 3); Benin (n = 2); Central African Republic (n = 2); Mali (n = 2); Mauritius (n = 2); Botswana (n = 1); Cote d’Ivoire (n = 1); Ethiopia (n = 1); Guinea-Bissau (n = 1); Madagascar (n = 1); Mauritania (n = 1); South Sudan (n = 1); Swaziland (n = 1); Tanzania (n = 1); Uganda (n = 1); and Zimbabwe (n = 1).

Middle East and Central Asia included 19 countries: Indonesia (n = 18); United Arab Emirates (n = 14); Israel (n = 13); Kazakhstan (n = 9); Pakistan (n = 8); Turkey (n = 8); Iran (n = 7); Saudi Arabia (n = 6); Bahrain (n = 3); Lebanon (n = 3); Jordan (n = 2); Kyrgyzstan (n = 2); Palestinian Territories (n = 2); Qatar (n = 2); Turkmenistan (n = 2); Afghanistan (n = 1); Iraq (n = 1); Kuwait (n = 1); and Syria (n = 1).

We investigated how effects of political orientation on partner preferences differed between four different regions. Namely, these were Europe (n = 7,417), Latin and South America (n = 3,325), North America (n = 1,592), and South and East Asia (n = 542). We could not include Oceania (n = 170), Africa (n = 108), and Middle East and Central Asia (n = 103) because sample sizes were too small (n < 500) to reach any conclusions.

regions = regions %>% filter(participants > 500)
data_included_documented_reg = data_included_documented %>%
  filter(region_final %in% regions$region_final)

regions_reg =
  data_included_documented_reg %>%
  select(region_final, country) %>%
  table() %>%
  as.data.frame() %>%
  filter(Freq != 0) %>%
  arrange(-Freq)


regions_reg

## # A tibble: 94 × 3
##    region_final            country                   Freq
##    <fct>                   <fct>                    <int>
##  1 Europe                  France                    2013
##  2 Europe                  Germany                   1846
##  3 North America           United States of America  1254
##  4 Latin and South America Mexico                    1157
##  5 Europe                  Italy                      968
##  6 Latin and South America Brazil                     806
##  7 Europe                  Spain                      562
##  8 Europe                  United Kingdom             499
##  9 Europe                  Denmark                    395
## 10 Latin and South America Colombia                   387
## # ℹ 84 more rows

Models

S1 Interest in Single Life

data_included_documented_reg_wide = data_included_documented_reg %>%
  pivot_wider(names_from = region_final, values_from = political_orientation) %>%
  select(interest_single, Europe, 'South and East Asia', 'Latin and South America', 'North America')

models_interest_single = data_included_documented_reg_wide %>%
  select(-interest_single) %>%
  map(~lm(scale(data_included_documented_reg_wide$interest_single) ~ scale(.x),
      data = data_included_documented_reg_wide)) %>%
  map(lm.beta)

models_interest_single_coef = models_interest_single %>%
  map(coef) %>%
  as.data.frame() %>%
  rownames_to_column(var = "rowname") %>%
  filter(rowname != "(Intercept)") %>%
  pivot_longer(cols = -rowname) %>%
  select(-rowname) %>%
  rename(mean = value)

models_interest_single_se = models_interest_single %>%
  map(tidy) %>%
  tibble(models_pref_politicalsim_lin_se = ., Names = names(.)) %>%
  hoist(models_pref_politicalsim_lin_se, coefficients = "std.error") %>%
  select(-models_pref_politicalsim_lin_se) %>%
  unnest_wider(., coefficients, names_sep = "_") %>%
  select(coefficients_2, Names) %>%
  rename("name" = "Names",
         "se" = "coefficients_2") %>%
   mutate(name = ifelse(name == "South and East Asia",
                       "South.and.East.Asia",
                       ifelse(name == "Latin and South America",
                       "Latin.and.South.America",
                       ifelse(name == "North America",
                       "North.America",
                       name))))

models_interest_single_analyses = left_join(models_interest_single_coef,
                                            models_interest_single_se,
                                            by = "name") %>%
  mutate(outcome = "S1 Interest in Single Life")

countries_reg =
  data_included_documented_reg %>%
  filter(!is.na(interest_single)) %>%
  select(region_final) %>%
  table() %>%
  as.data.frame() %>%
  arrange(-Freq)


models_interest_single_analyses$n = countries_reg$Freq
sum(models_interest_single_analyses$n)

## [1] 12830

model = mvmeta(mean ~ 1, data = models_interest_single_analyses, S = se^2,
               method = "fixed")
summary(model)

## Call:  mvmeta(formula = mean ~ 1, S = se^2, data = models_interest_single_analyses, 
##     method = "fixed")
## 
## Univariate fixed-effects meta-analysis
## Dimension: 1
## 
## Fixed-effects coefficients
##              Estimate  Std. Error        z  Pr(>|z|)  95%ci.lb  95%ci.ub     
## (Intercept)   -0.0607      0.0087  -6.9773    0.0000   -0.0778   -0.0437  ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 
## 
## Univariate Cochran Q-test for heterogeneity:
## Q = 16.4400 (df = 3), p-value = 0.0009
## I-square statistic = 81.8%
## 
## 4 studies, 4 observations, 1 fixed and 0 random-effects parameters
##  logLik      AIC      BIC  
##  3.5018  -5.0037  -5.6174

S2 Interest in Sexual, Non-Romantic Relationships

data_included_documented_reg_wide = data_included_documented_reg %>%
  pivot_wider(names_from = region_final, values_from = political_orientation) %>%
  select(interest_sexrel, Europe, 'South and East Asia', 'Latin and South America', 'North America')

models_interest_sexrel = data_included_documented_reg_wide %>%
  select(-interest_sexrel) %>%
  map(~lm(scale(data_included_documented_reg_wide$interest_sexrel) ~ scale(.x),
          data = data_included_documented_reg_wide)) %>%
  map(lm.beta)

models_interest_sexrel_coef = models_interest_sexrel %>%
  map(coef) %>%
  as.data.frame() %>%
  rownames_to_column(var = "rowname") %>%
  filter(rowname != "(Intercept)") %>%
  pivot_longer(cols = -rowname) %>%
  select(-rowname) %>%
  rename(mean = value)

models_interest_sexrel_se = models_interest_sexrel %>%
  map(tidy) %>%
  tibble(models_pref_politicalsim_lin_se = ., Names = names(.)) %>%
  hoist(models_pref_politicalsim_lin_se, coefficients = "std.error") %>%
  select(-models_pref_politicalsim_lin_se) %>%
  unnest_wider(., coefficients, names_sep = "_") %>%
  select(coefficients_2, Names) %>%
  rename("name" = "Names",
         "se" = "coefficients_2") %>%
  mutate(name = ifelse(name == "South and East Asia",
                       "South.and.East.Asia",
                       ifelse(name == "Latin and South America",
                              "Latin.and.South.America",
                              ifelse(name == "North America",
                                     "North.America",
                                     name))))

models_interest_sexrel_analyses = left_join(models_interest_sexrel_coef,
                                            models_interest_sexrel_se,
                                            by = "name") %>%
  mutate(outcome = "S1 Interest in Single Life")

countries_reg =
  data_included_documented_reg %>%
  filter(!is.na(interest_sexrel)) %>%
  select(region_final) %>%
  table() %>%
  as.data.frame() %>%
  arrange(-Freq)


models_interest_sexrel_analyses$n = countries_reg$Freq
sum(models_interest_sexrel_analyses$n)

## [1] 12816

model = mvmeta(mean ~ 1, data = models_interest_sexrel_analyses, S = se^2,
               method = "fixed")
summary(model)

## Call:  mvmeta(formula = mean ~ 1, S = se^2, data = models_interest_sexrel_analyses, 
##     method = "fixed")
## 
## Univariate fixed-effects meta-analysis
## Dimension: 1
## 
## Fixed-effects coefficients
##              Estimate  Std. Error       z  Pr(>|z|)  95%ci.lb  95%ci.ub     
## (Intercept)    0.0392      0.0086  4.5559    0.0000    0.0223    0.0561  ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 
## 
## Univariate Cochran Q-test for heterogeneity:
## Q = 30.3133 (df = 3), p-value = 0.0000
## I-square statistic = 90.1%
## 
## 4 studies, 4 observations, 1 fixed and 0 random-effects parameters
##  logLik      AIC      BIC  
## -3.4338   8.8677   8.2539

S3 Interest in Non-Monogamous Relationships

data_included_documented_reg_wide = data_included_documented_reg %>%
  pivot_wider(names_from = region_final, values_from = political_orientation) %>%
  select(interest_nonmonrel, Europe, 'South and East Asia', 'Latin and South America', 'North America')

models_interest_nonmonrel = data_included_documented_reg_wide %>%
  select(-interest_nonmonrel) %>%
  map(~lm(scale(data_included_documented_reg_wide$interest_nonmonrel) ~ scale(.x),
          data = data_included_documented_reg_wide)) %>%
  map(lm.beta)

models_interest_nonmonrel_coef = models_interest_nonmonrel %>%
  map(coef) %>%
  as.data.frame() %>%
  rownames_to_column(var = "rowname") %>%
  filter(rowname != "(Intercept)") %>%
  pivot_longer(cols = -rowname) %>%
  select(-rowname) %>%
  rename(mean = value)

models_interest_nonmonrel_se = models_interest_nonmonrel %>%
  map(tidy) %>%
  tibble(models_pref_politicalsim_lin_se = ., Names = names(.)) %>%
  hoist(models_pref_politicalsim_lin_se, coefficients = "std.error") %>%
  select(-models_pref_politicalsim_lin_se) %>%
  unnest_wider(., coefficients, names_sep = "_") %>%
  select(coefficients_2, Names) %>%
  rename("name" = "Names",
         "se" = "coefficients_2") %>%
  mutate(name = ifelse(name == "South and East Asia",
                       "South.and.East.Asia",
                       ifelse(name == "Latin and South America",
                              "Latin.and.South.America",
                              ifelse(name == "North America",
                                     "North.America",
                                     name))))

models_interest_nonmonrel_analyses = left_join(models_interest_nonmonrel_coef,
                                            models_interest_nonmonrel_se,
                                            by = "name") %>%
  mutate(outcome = "S1 Interest in Single Life")

countries_reg =
  data_included_documented_reg %>%
  filter(!is.na(interest_nonmonrel)) %>%
  select(region_final) %>%
  table() %>%
  as.data.frame() %>%
  arrange(-Freq)


models_interest_nonmonrel_analyses$n = countries_reg$Freq
sum(models_interest_nonmonrel_analyses$n)

## [1] 12772

model = mvmeta(mean ~ 1, data = models_interest_nonmonrel_analyses, S = se^2,
               method = "fixed")
summary(model)

## Call:  mvmeta(formula = mean ~ 1, S = se^2, data = models_interest_nonmonrel_analyses, 
##     method = "fixed")
## 
## Univariate fixed-effects meta-analysis
## Dimension: 1
## 
## Fixed-effects coefficients
##              Estimate  Std. Error        z  Pr(>|z|)  95%ci.lb  95%ci.ub     
## (Intercept)   -0.0597      0.0087  -6.8974    0.0000   -0.0767   -0.0427  ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 
## 
## Univariate Cochran Q-test for heterogeneity:
## Q = 9.0060 (df = 3), p-value = 0.0292
## I-square statistic = 66.7%
## 
## 4 studies, 4 observations, 1 fixed and 0 random-effects parameters
##   logLik       AIC       BIC  
##   7.1120  -12.2240  -12.8377

S4 Interest in Monogamous Relationships

data_included_documented_reg_wide = data_included_documented_reg %>%
  pivot_wider(names_from = region_final, values_from = political_orientation) %>%
  select(interest_monrel, Europe, 'South and East Asia', 'Latin and South America', 'North America')

models_interest_monrel = data_included_documented_reg_wide %>%
  select(-interest_monrel) %>%
  map(~lm(scale(data_included_documented_reg_wide$interest_monrel) ~ scale(.x),
          data = data_included_documented_reg_wide)) %>%
  map(lm.beta)

models_interest_monrel_coef = models_interest_monrel %>%
  map(coef) %>%
  as.data.frame() %>%
  rownames_to_column(var = "rowname") %>%
  filter(rowname != "(Intercept)") %>%
  pivot_longer(cols = -rowname) %>%
  select(-rowname) %>%
  rename(mean = value)

models_interest_monrel_se = models_interest_monrel %>%
  map(tidy) %>%
  tibble(models_pref_politicalsim_lin_se = ., Names = names(.)) %>%
  hoist(models_pref_politicalsim_lin_se, coefficients = "std.error") %>%
  select(-models_pref_politicalsim_lin_se) %>%
  unnest_wider(., coefficients, names_sep = "_") %>%
  select(coefficients_2, Names) %>%
  rename("name" = "Names",
         "se" = "coefficients_2") %>%
  mutate(name = ifelse(name == "South and East Asia",
                       "South.and.East.Asia",
                       ifelse(name == "Latin and South America",
                              "Latin.and.South.America",
                              ifelse(name == "North America",
                                     "North.America",
                                     name))))

models_interest_monrel_analyses = left_join(models_interest_monrel_coef,
                                            models_interest_monrel_se,
                                            by = "name") %>%
  mutate(outcome = "S1 Interest in Single Life")

countries_reg =
  data_included_documented_reg %>%
  filter(!is.na(interest_monrel)) %>%
  select(region_final) %>%
  table() %>%
  as.data.frame() %>%
  arrange(-Freq)


models_interest_monrel_analyses$n = countries_reg$Freq
sum(models_interest_monrel_analyses$n)

## [1] 12791

model = mvmeta(mean ~ 1, data = models_interest_monrel_analyses, S = se^2,
               method = "fixed")
summary(model)

## Call:  mvmeta(formula = mean ~ 1, S = se^2, data = models_interest_monrel_analyses, 
##     method = "fixed")
## 
## Univariate fixed-effects meta-analysis
## Dimension: 1
## 
## Fixed-effects coefficients
##              Estimate  Std. Error        z  Pr(>|z|)  95%ci.lb  95%ci.ub   
## (Intercept)   -0.0182      0.0086  -2.1055    0.0353   -0.0351   -0.0013  *
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 
## 
## Univariate Cochran Q-test for heterogeneity:
## Q = 9.4189 (df = 3), p-value = 0.0242
## I-square statistic = 68.1%
## 
## 4 studies, 4 observations, 1 fixed and 0 random-effects parameters
##   logLik       AIC       BIC  
##   7.1469  -12.2938  -12.9075